Unification of Spacial Dimensions Theory
While the nature of mass and quantum spin is appreciably mystifying, the nature of spacial dimension itself is taken for granted. We intuitively use Descartes’ Cartesian-coordinates to represent spacial quality with 3-axes. This should beg the question however, as to why there appears to be 3 spacial qualities. Why not 2, or 4? It could be said that the spacial dimensions are an arbitrary rendering presented to our conscious experience: a phenomenon as opposed to a noumenon. Thus, we shall propose a theoretical framework of space, a unifying spacial quality of the universe that does not require an arbitrary number of dimensions. This creates the illusion of space and time. We will demote the Euclidean-cartesian model of space to a configuration space and will determine that it just a reflection of our perception.
Occam’s razor requires the absolute definition of speculation being that which most elegantly matches our sensation. This means a theory should reduce its dependence on hidden variables that do not need to be there. For example, we should assume that \(4=4\), and not \(4=4+1-1\). However, speculation is therefore dependent on our sensations which may be wrong. Sensations do not necessarily represent a physical system in its true form. Instead, sensations are merely a subjective rendering (the act of making sense) of signals coming from the outside world. Occam’s razor is rendered a useless means to develop a theory for the mechanism in which a particle can interact with itself given that we have no natural sense of such mechanics. From Occam’s point of view, our sensations do not reflect reality in its true form, therefore a theory should not rely on them. We should not assume that our sensation of spacial quality is a reflection of spacial quality in and of itself. We should assume the position of Plato’s cave.
What is a theory of spacial quality that satisfies Occam’s razor? Suppose space truly has 3 dimensions. What is the mechanism in which 3 spacial dimensions should arise as opposed to any other number of spacial dimensions? It was not enough to shrug our shoulders when poised to explain the quantised orbits of Bohr’s atom, nor should we when poised to explain the apparent number of spacial dimensions. Given that our sensations are not a reliable indicator of the nature of things, we need to include this in a theory. If we can produce a theory that unifies the 3 spacial dimensions and time as a single quality, we should adopt it.
Unification of Distance, Time, Velocity, and Mass.
While this concept is often reiterated in discussions of General and Special Relativity, it is crucial to reiterate here. Distance and time are “two sides of the same coin”. Time is the expression of a traversal of distance and distance is the expression of the time taken to traverse. The constant is naturally \(c\), meaning the absolute, universal rate of change. Velocity is therefore a macroscopic phenomena of things that do not appear to travel at \(c\) virtue of their mass. Velocity and mass are inversely proportional.
Faculty & Instancy
Let us make as few assumptions as possible and let us not assume that spacial quality is a matter of making sense of an untouched, underlying configuration space.
A Configuration Space to Euclidean Space
Now let us propose an instance of gravitation \(A\), and an instance of \(+1\) charged particle, \(B\) separated by a distance/time of 1 meter.
| Particle | Mass | Charge |
| \(A\) | \(1kg\) | \(0\) |
| \(B\) | \(0\) | \(+1e\) |
| Interval | Distance | Time |
| \(AB\) | \(1m\) |
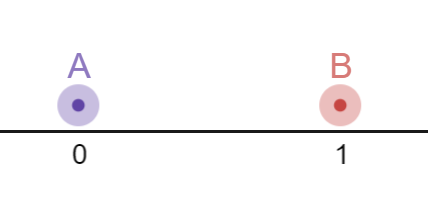
\(A\) is a gravitational instance and thus, its effect on \(B\) will be a characteristic attraction. The distance between
\(A\) and \(B\) will thus be reduced over time. In isolation, this interaction can be represented by a single spacial dimension.
Now suppose that a third instance \(C\) is introduced to the system, however it’s chargeless and massless, thus is not affected by either force. It’s distance however, maintains 0.5 units between each.
| Particle | Mass | Charge |
| \(A\) | \(0\) | \(-1e\) |
| \(B\) | \(1kg\) | \(1e\) |
| \(C\) | \(0\) | \(0\) |
| Interval | Distance | Time |
| \(AB\) | \(1m\) | |
| \(CA\) | \(0.5m\) | |
| \(CB\) | \(0.5m\) |
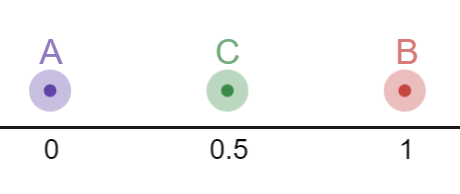
\(A\) must approach \(B\), but \(C\) cannot approach either. In other words, \(AB\) must decrease while \(CA\) and \(CB\) must remain the same distance. This seems impossible in 1 spacial dimension, yet it must occur. The brain can only speak in sensations including the sensation of space itself. In a feat of cognitive genius, the brain renders this contradiction in the form of a 2-dimensional construct.
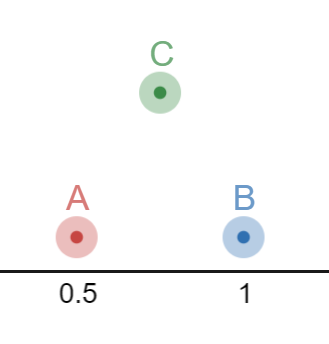
\(C\) extends into a new vertical dimension in order to maintain the information of these distinct, but uncompromising distances.
Now let us make \(C\) a negative charge itself.
| Particle | Mass | Charge |
| \(A\) | \(0\) | \(-1e\) |
| \(B\) | \(1kg\) | \(1e\) |
| \(C\) | \(0\) | \(-1e\) |
Now we have a situation where both \(A\) and \(C\) must approach \(B\), however \(C\) must repel \(A\). In other words, \(AB\) and \(CB\) must decrease, but \(AC\) must increase simultaneously. This is impossible if we are to represent this 2-dimensionally. Alas, 3-dimensional rendering solves the problem.
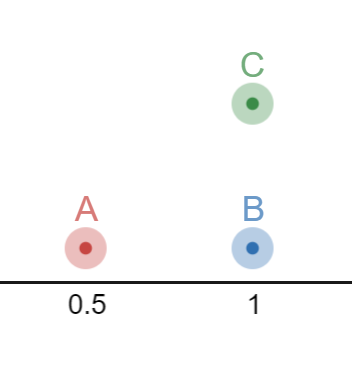
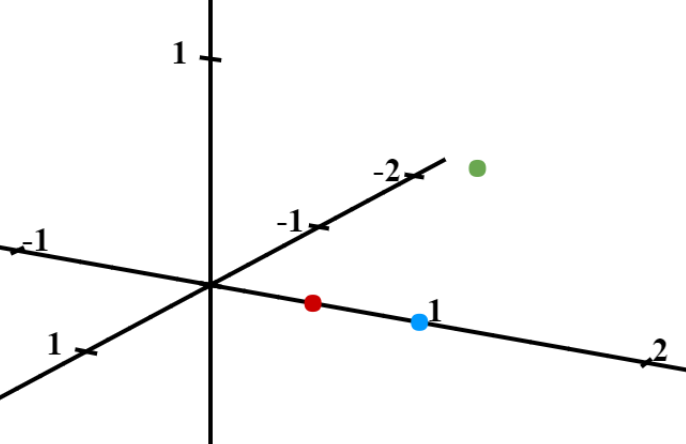
\(C\) has been pushed into another spacial dimension in order to simultaneously maintain the attraction and repulsion.